这一系列博文我们对 Diffusion 模型进行简单的介绍 :)
我们认为比较重要的 Paper List：
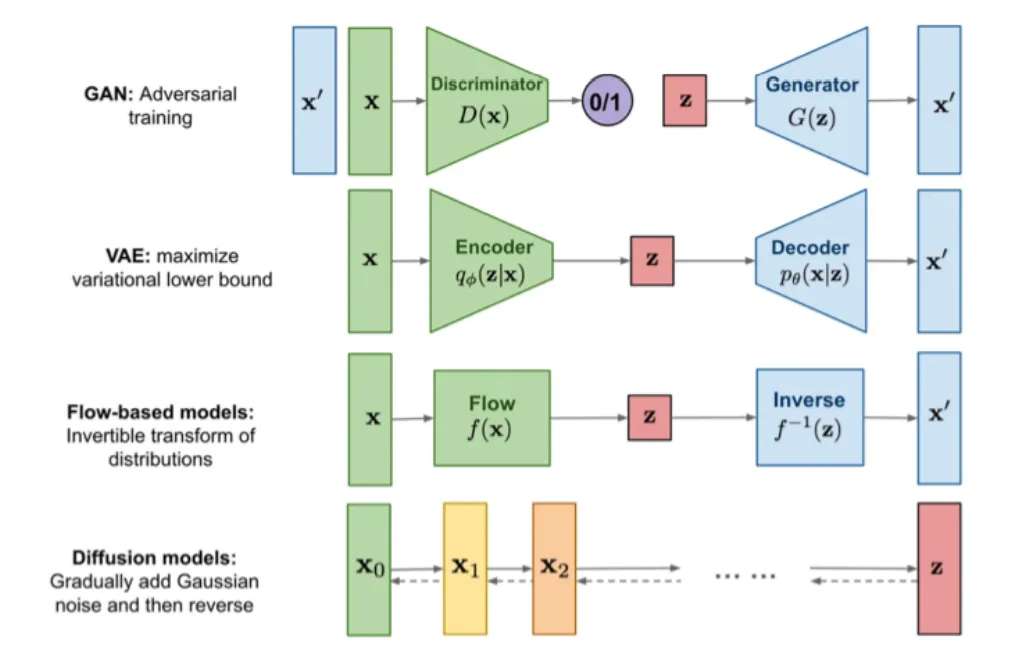
- 重新回顾 Diffusion：更具多样性的生成式模型
- [1503.03585] Deep Unsupervised Learning using Nonequilibrium Thermodynamics (ICML’15)
- [2006.11239] Denoising Diffusion Probabilistic Models (NIPS’20)
- [2102.09672] Improved Denoising Diffusion Probabilistic Models (ICML’21)
- [2010.02502] Denoising Diffusion Implicit Models (ICLR’21)
- [2106.15282] Cascaded Diffusion Models for High Fidelity Image Generation (JMLR)
- [2104.07636] Image Super-Resolution via Iterative Refinement (TPAMI)
- 为生成添加引导
- [2105.05233] Diffusion Models Beat GANs on Image Synthesis (NIPS’21)
- [2112.10741] GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models (ICML’22)
- [2207.12598] Classifier-Free Diffusion Guidance (NIPS’21 Workshop)
- Departure to Latent Space
- [2112.10752] High-resolution image synthesis with latent diffusion models (CVPR’22 Oral)
- [2302.05543] Adding Conditional Control to Text-to-Image Diffusion Models
- [2204.06125] Hierarchical Text-Conditional Image Generation with CLIP Latents (DALL·E 2)
- [2205.11487] Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding (NIPS’22, Imagen)
- 未分类（还没读，咕咕咕）
- Zero-Shot Contrastive Loss for Text-Guided Diffusion Image Style Transfer
DDPM
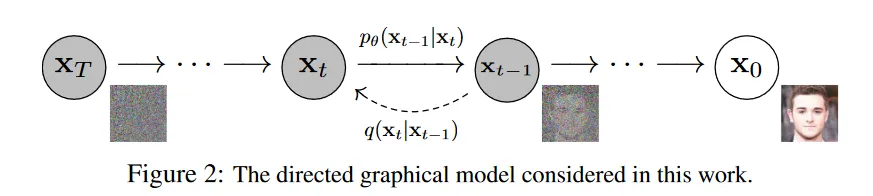
DDPM（Denoising Diffusion Probabilistic Models）是一种生成式模型，其可以将噪声 $\mathbf{x}_T$ 经过一系列级联的去噪（Denoising）过程生成具有真实感的图像 $\mathbf{x}_0$。
在 DDPM 中，具有两个重要的过程：前向过程（forward process, or diffusion process）和去噪过程（denoising process）：
前向过程
前向过程，也就是图中的 $q$ 过程，通过不断加高斯噪音的方式将原始数据分布 $q(\mathbf{x}_0)$ 转换为简单易处理的标准正态分布。在前向过程中，一个初始的噪声图像 $\mathbf{x}_T$ 被迭代地与一系列高斯噪声进行混合，生成一系列经过随机扰动的图像 $\mathbf{x}_t$，其中 $t=T-1,T-2,\ldots,0$。
更加形式化地，我们可以表示为：
$$q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right):=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right)
$$
这里 $q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)$ 表示隐变量 $\mathbf{x}_t$ 相对于 $\mathbf{x}_{t-1}$ 的条件概率分布。也就是说，如果我们已知隐变量 $\mathbf{x}_{t-1}$ 的取值，想要获得隐变量 $\mathbf{x}_t$ 的取值，我们就要从这个关于 $\mathbf{x}_t$ 的正态分布中采样，其均值为 $\sqrt{1-\beta_t}\mathbf{x}_{t-1}$，方差为 $\beta_t\mathbf{I}$。这里的数列 ${\beta_t}$ 由人工手动定义，在原文的实现中实现为在 $\beta_1=10^{-4}$ 到 $\beta_T=0.02$ 的线性插值，这里 $T=1000$。直观上，每一步前向过程的操作就是对输入的数据加入高斯噪声的扰动。
在该算法中，从原始图片输入 $\mathbf{x}_0$ 到完全的高斯噪声 $\mathbf{x}_T$ 的过程是由一系列 $q$ 过程级联产生的。我们认为这个级联后的过程是一个马尔科夫过程，这意味着在任意时间 $t$，当前状态 $\mathbf{x}_t$ 的条件概率分布只依赖于其前一个状态 $\mathbf{x}_{t-1}$，即：
$$q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_{t-2}, \ldots, \mathbf{x}_0\right)=q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)
$$
这里 $q(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_{t-2}, \ldots, \mathbf{x}_0)$ 表示在给定之前的所有状态的条件下，当前状态 $\mathbf{x}_t$ 的条件概率分布，$q(\mathbf{x}_t \mid \mathbf{x}_{t-1})$ 表示当前状态 $\mathbf{x}_t$ 相对于 $\mathbf{x}_{t-1}$ 的条件概率分布。根据马尔科夫过程的性质，我们有：
$$q(\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_T \mid \mathbf{x}_0) =\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)
$$
这里 $q(\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_T \mid \mathbf{x}_0)$ 表示隐变量 $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_T$（之后简记为 $\mathbf{x}_{1:T}$）相对于 $\mathbf{x}_0$ 的联合条件概率分布。
同时，根据高斯分布的可叠加性，我们可以得出：
$$q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right),
$$
这里 $\alpha_t:=1-\beta_t$, $\bar{\alpha}_t:=\prod_{s=1}^t \alpha_s$。
去噪过程
我们希望去噪过程是上述前向过程的逆过程，也就是说，我们要获得 $q(\mathbf{x}_t \mid \mathbf{x}_{t-1})$ 的逆分布。我们知道，如果 $q(\mathbf{x}_t \mid \mathbf{x}_{t-1})$ 是正态分布且 $\beta_t$ 足够接近 0，那么其逆过程也近似为一个正态分布。我们通过一个神经网络 $\theta$ 来拟合这个正态分布的均值（与方差，Improved DDPM）。
$$p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right):=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)
$$
如果这个网络 $\theta$ 被成功训练到可以拟合 $p$ 过程，那么我们就具有了一个具有“去噪”能力的网络。进而，我们可以从标准正态分布中采样 $\mathbf{x}_T$，然后经过 $T$ 次 $p_\theta$ 的变换，便得到了具有真实感的图像 $\mathbf{x}_0$。
马尔可夫过程保证了：
$$p_\theta\left(\mathbf{x}_{0: T}\right):=p\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)
$$
训练过程
训练的目标是通过模型生成的数据分布 $p_\theta(\mathbf{x}_0)$ 与真实数据分布 $q(\mathbf{x}_0)$ 尽可能相近。这可以通过最小化假设检验 $\mathbb{E}\left[-\log p_\theta\left(\mathbf{x}_0\right)\right]$ 来实现。由于：
$$\begin{aligned}
p_\theta\left(\boldsymbol{x}_0\right) & =\int p_\theta\left(\boldsymbol{x}_{0: T}\right) d \boldsymbol{x}_{1: T}\\
p_\theta\left(\boldsymbol{x}_{0: T}\right) & =p_\theta\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_\theta\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)
\end{aligned}
$$
我们尝试去推出 $\mathbb{E}\left[-\log p_\theta\left(\mathbf{x}_0\right)\right]$ 的上界，通过将其上界优化小的方式去优化该假设检验值：
$$\begin{aligned}
\mathcal{L}_{c e} & =-\mathbb{E}_{q\left(\boldsymbol{x}_0\right)}\left(\log p_\theta\left(\boldsymbol{x}_0\right)\right) \\
& =-\mathbb{E}_{q\left(\boldsymbol{x}_0\right)}\left(\log \int p_\theta\left(\boldsymbol{x}_{0: T}\right) d \boldsymbol{x}_{1: T}\right) \\
& =-\mathbb{E}_{q\left(\boldsymbol{x}_0\right)}\left(\log \int q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right) \frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)} d \boldsymbol{x}_{1: T}\right) \\
& =-\mathbb{E}_{q\left(\boldsymbol{x}_0\right)}\left(\log \mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left(\frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\right)\right) \\
& \leq-\mathbb{E}_{q\left(\boldsymbol{x}_0\right)}\left(\mathbb{E}_{q\left(\boldsymbol{x}_{1: T \mid} \mid \boldsymbol{x}_0\right)}\left(\log \frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\right)\right) \\
& =-\iint q\left(\boldsymbol{x}_0\right) q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right) \log \frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)} d \boldsymbol{x}_0 d \boldsymbol{x}_{1: T} \\
& =-\int q\left(\boldsymbol{x}_{0: T}\right) \log \frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)} d \boldsymbol{x}_{0: T} \\
& =-\mathbb{E}_{q\left(\boldsymbol{x}_{0: T}\right)}\left[\log \frac{p_\theta\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\right]=\mathbb{E}_{q\left(\boldsymbol{x}_{0: T}\right)}\left[\log \frac{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}{p_\theta\left(\boldsymbol{x}_{0: T}\right)}\right]
\end{aligned}
$$
这里用了变分自编码器（VAE）中的重要不等式，通常称为“ELBO（evidence lower bound）不等式”。下面对式子进行解释：
左边的期望值是关于潜在变量 $\mathbf{z}$ 的先验分布 $p(\mathbf{z})$ 取期望后的结果，其中 $\mathbf{z}$ 通过生成模型 $p_\theta(\mathbf{x}_0, \mathbf{z})$ 与观测变量 $\mathbf{x}_0$ 相关联。根据贝叶斯定理，我们有：
$$p_\theta\left(\mathbf{x}_0, \mathbf{z}\right)=p_\theta\left(\mathbf{x}_0 \mid \mathbf{z}\right) p(\mathbf{z})
$$
因此，可以将左边的期望值写成以下形式：
$$\mathbb{E}\left[-\log p_\theta\left(\mathbf{x}_0\right)\right]=\mathbb{E}_{p(\mathbf{z})}\left[-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{z}\right)\right]-\mathbb{H}[p(\mathbf{z})]
$$
其中，$\mathbb{H}\left[p(\mathbf{z})\right]$ 是潜在变量的先验分布 $p(\mathbf{z})$ 的熵，可以看作是潜在变量的不确定度的度量。在我们的例子中，潜在变量 $\mathbf{z}$ 为 $\mathbf{x}_{1:T}$。
接下来我们用马尔科夫过程的性质把 $\mathbb{E}_{q\left(\boldsymbol{x}_{0: T}\right)}\left[\log \frac{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}{p_\theta\left(\boldsymbol{x}_{0: T}\right)}\right]$ 中的联合概率分布拆开。同时，因为 $q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)$ 的分布的 closed-form solution 不可知，我们引入 $\mathbf{x}_0$ 后利用贝叶斯公式可以转换成 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)$，这个分布的参数为：
$$q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) \\
\text{where} \quad \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right):=\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0+\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t \quad \\
\text{and} \quad \tilde{\beta}_t:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t
$$
最终我们发现上述上界等价于：
$$\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t>1} \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}} \underbrace{-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}]
$$
我们希望的优化目标，便是这些概率分布之间的 KL 散度。
优化目标的进一步改进
我们考虑 $L_{t-1}$，由于计算 KL 散度的两个分布都是正态分布，我们可以直接得到闭式解：
$$\begin{aligned}
\mathcal{L}_{t-1} =\mathbb{E}_{q\left(\boldsymbol{x}_0, \boldsymbol{x}_t\right)}\left[\frac{1}{2 \sigma_t^2}\left\|\tilde{\boldsymbol{\mu}}\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right)-\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)\right\|^2\right]+C
\end{aligned}
$$
这相当于直接预测 $p_\theta$ 过程的均值。
而由于我们在训练过程中知道前向过程 $\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}$，且在训练过程中要将 $\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)$ 回归到的值只与 $\boldsymbol{x}_0$ 和 $\boldsymbol{x}_t$ 有关，于是我们可以代入消去这个回归值中的 $\boldsymbol{x}_0$，得到我们要把 $\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)$ 回归到：
$$\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}\right)
$$
而这里的 $\boldsymbol{x}_t$ 是 $\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)$ 的输入。本着简便的原则，我们可以设计：
$$\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right) = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\boldsymbol{x}_t, t\right)\right)
$$
也就是说，我们的网络 $\boldsymbol{\epsilon}_\theta$ 最终只需要输入 $\boldsymbol{x}_t$ 和当前时间的 time embedding，输出我们在前向过程中相对原图添加的噪声即可。
于是我们可以对 Loss 稍作修改：
$$\mathbb{E}_{\mathbf{x}_0, \epsilon}\left[\frac{\beta_t^2}{2 \sigma_t^2 \alpha_t\left(1-\bar{\alpha}_t\right)}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right]
$$
再简便一些，我们丢弃前面的系数：
$$L_{\text {simple }}(\theta):=\mathbb{E}_{t, \mathbf{x}_0, \epsilon}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right]
$$
这相当于对于不同时间步的 Loss 做了一个分配不同权重的操作。事实上，这里将 $t$ 较小的时间步的 Loss 权重降低，使得模型不用花费太多精力在考虑 fine-grained 的细节上。
Reference
除了原论文外，本节内容的整理我们参考了以下内容：
感觉水够一篇的篇幅了，换一篇接着写 :)